There have been many Gladiacoin Reviews written by individuals that have pulled information from the Gladiacoin website and provided you with their opinions of Gladiacoin only to recommend a program or business that they want you to join. This Gladiacoin Review will reveal what is really happening and how members are being paid from Gladiacoin.
What is Gladiacoin?
Gladiacoin is a Bitcoin Trading Platform. Where you can Double Your Bitcoins in 90 Days. You can do this passively or aggressively. You Double Your Bitcoins Passively by Choosing one of Glaidicoin Packages that will double your Bitcoins in 90 Days, and wait for your Bitcoin to double. You grow your Bitcoins aggressively by participating in Gladiacoin’s Binary Network where you tell others about Gladiacoin. Gladiacoin does not pay you for referring others, they pay you based upon the Bitcoin volume generated by those that you refer.
What is a Bitcoin?
Watch the video below of an interview of Andreas Antonopoulos who is considered an expert on Bitcoins:
Gladicoin Packages
Gladiacoin has six packages to chose from for you to double your Bitcoins in 90 Days ranging from Spartacus 2 through Spartacus 7. There is a seventh package (Spartacus 1) where your Bitcoins do not double. Some members of Gladiacoin use the Spartacus 1 Package to hold their position in the Binary Network until they can upgrade to one of the other six Spartacus Packages.
How Much Does It Cost to Join Gladiacoin?
The price of a Bitcoin determines how much it will cost you to join Gladiacoin. There are many places online where you can find the price of a Bitcoin. I use a Bitcoin Calculator because it tells me how much I will pay in the currency that I am using to purchase my Bitcoins. As of the writing of this review the price for 0.05 Bitcoin and 1 Bitcoin is below:


A small price change in the short time between image captures
Using the above as your baseline figure for a Bitcoin you can get an idea of what it will cost to join Gladiacoin based on the following Packages. The price of a Bitcoin can be more or less than the figures above. That amount that you pay to get started depends upon the price of a Bitcoin on the day and time that you purchase your Bitcoins.
- Spartacus 1 – 0.05 Bitcoin – Does not Double In 90 Days
- Spartacus 2 – 0.1 Bitcoin – Doubles to 0.2 Bitcoin in 90 Days (approx. $108.84)
- Spartacus 3 – 0.3 Bitcoin – Doubles to 0.6 Bitcoin in 90 Days (approx. $326.52)
- Spartacus 4 – 0.5 Bitcoin – Doubles to 1 Bitcoin in 90 Days (approx. $544.20)
- Spartacus 5 – 1 Bitcoin – Doubles to 2 Bitcoins in 90 Days
- Spartacus 6 – 2 Bitcoins – Doubles to 4 Bitcoins in 90 Days
- Spartacus 7 – 4 Bitcoins – Doubles to 8 Bitcoins in 90 Days
How Does Gladiacoin Make Money?
Gladiacoin has a staff of Bitcoin Traders that buys and sells Bitcoins on a daily basis. There are many Bitcoin Exchanges on the internet, Gladiacoin Trades buys from one exchange that is selling Bitcoins for a lower price and sells to another exchange that is buying for a higher price. They take the difference in the price of the Bitcoins sold and share that with all Gladiacoin members that are participating in one of the Spartacus Packages that is doubling in 90 days.
Ex: Bitcoin Exchange ABC is selling Bitcoins for $600, and Bitcoin Exchange XYZ is buying Bitcoins for $700. A Gladiacoin Trader will buy as many Bitcoins from Exchange ABC and sell them to Exchange XYZ. The $100 per Bitcoin Profit goes into Gladiacoin’s account and every day, they pay their members with Spartacus 2 – Spartacus 7 accounts 2.2 percent profit.
Example of Daily Trader Bonus Profit Sharing
Every day Gladiacoin pays it members with a Spartacus 2 – Spartacus 7 Package a Trader Bonus of 2.2 percent. This bonus helps the Bitcoins in the members account double in 90 Days. Below is a screen shot of a Spartacus 2 Package Statement showing the daily Trader Bonus being added to the account:
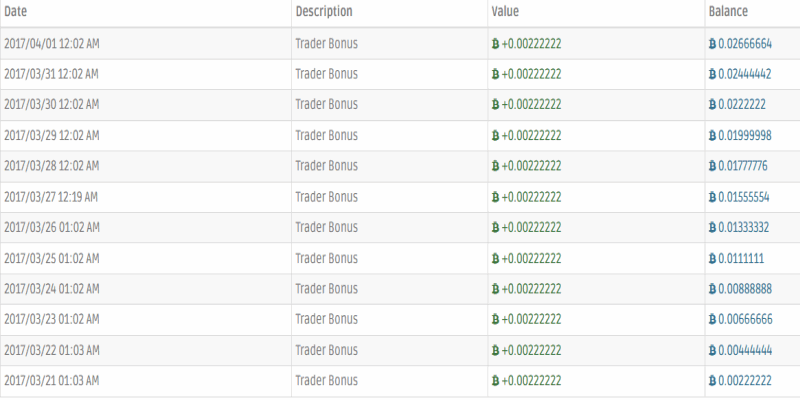
When the members account reaches 0.03 bitcoin, Gladiacoin will transfer the Bitcoin to the members Bitcoin Wallet. This is how Gladiacoin members that don’t want to participate in Gladiacoin’s Binary Network can grow their Bitcoin passively and have them doubled in 90 days.
- Spartacus 2 Packages pays a member every 14 days
- Spartacus 3 Packages pays a member every 5 days
- Spartacus 4 Packages pays a member every 3 days
- Spartacus 5 Packages Pays a member every 2 days
- Spartacus 6 Packages Pays a member every day
- Spartacus 7 Packages Pays a member every day
The image below is of a Spartacus 4 Package that is participating in Gladiacoin’s Binary Network, and the member is receiving the daily 2.2 percent Trader Bonus and the 9 percent Binary Bonus to double his bitcoins in less than 90 days:

The Trader Bonuses are speeding up the doubling rate for this Spartacus 4 Package. Instead of getting paid every three days, this member is getting Bitcoin transferred to his Bitcoin wallet every two days. This is not typical because Binary Bonuses are only paid when you have Bitcoins being added to the Lower Leg of your Binary Network. Your Lower Leg is the leg of your Binary Network that has the least amount of Bitcoin volume in it.
Ex: There are 5 Spartacus 7 Packages purchased by members in your Left Binary Leg, and their are 10 Spartacus 7 Packages purchased by members in your Right Binary Leg. You have 20 Bitcoins (4 Bitcoins times 5 Packages) in your Left Binary Leg, and 40 Bitcoins (4 Bitcoins times 10 Packages) in your Right Binary Leg. Your Left Binary Leg is your Lower Leg because it has the least amount of Bitcoin Volume.
You will receive a Trader bonus of 1.8 Bitcoins (20 Bitcoins times 9 percent) if your had a Spartacus 4 Package based upon the example above.
- Spartacus 1 Pays a 5 Percent Binary Bonus
- Spartacus 2 Pays a 6 Percent Binary Bonus
- Spartacus 3 Pays a 7 Percent Binary Bonus
- Spartacus 4 Pays a 9 Percent Binary Bonus
- Spartacus 5 Pays a 11 Percent Binary Bonus
- Spartacus 6 Pays a 13 Percent Binary Bonus
- Spartacus 7 Pays a 15 Percent Binary Bonus
The image below is of the Bitcoin Wallet to show the transfer of Bitcoin earned at Gladiacoin to the members Bitcoin Wallet:

The Bitcoin amounts in blue match the amounts of Bitcoin earned from participating in the Gladiacoin Double Your Bitcoin in 90 Days opportunity.
Bitcoins are here to stay and there will only be a total of 21 million Bitcoins produced. As of 2016 there have been 15.6 million Bitcoins produced which represents 75 percent of the 21 million total. People that are participating in Gladiacoin are doing so to increase the amount of Bitcoins that they have in their possession. The stability of the market and the demand for Bitcoins will only drive the price for Bitcoins higher.
The Owners of Gladiacoin
Trying to find out who owns Gladiacoin is a difficult task. Some governments have outlawed Bitcoins in their countries, and for that reason the owners have decided not to make their personal information known.
If you view Gladiacoin as an investment, my advice to you it to treat it like any high risk investment that you want to use to increase the amount of money you have in your investment portfolio, don’t invest money that you can’t afford to lose.
Hopefully I have provided you with enough information in this Gladiacoin Review to make an educated decision about Gladiacoin. Regardless of what I have shared with you in this Gladiacoin Review, I highly recommend that you conduct your own due diligence to find out if Gladiacoin is an opportunity that you want to participate in.
For additional educational videos produced by Andreas Antonopoulos, click here >>Bitcoin Educational Platform<<






